Abstract
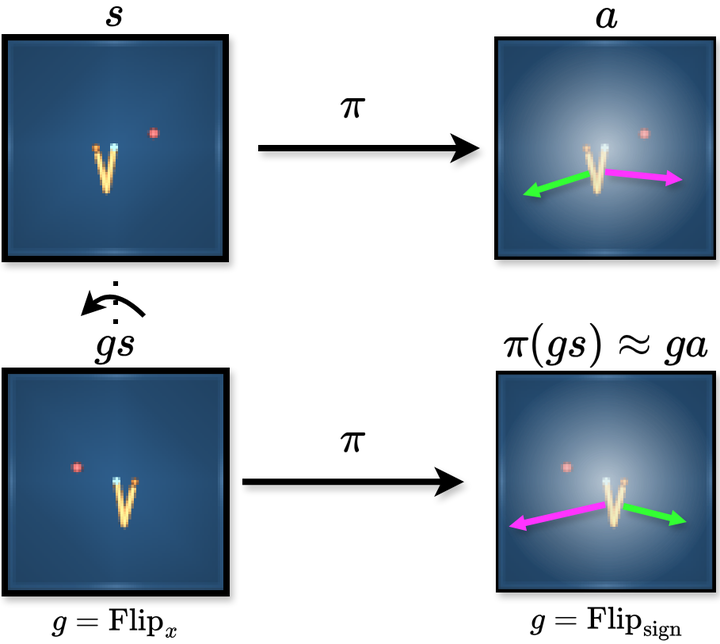
Equivariant neural networks have shown great success in reinforcement learning, improving sample efficiency and generalization when there is symmetry in the task. However, in many problems, only approximate symmetry is present, which makes imposing exact symmetry inappropriate. Recently, approximately equivariant networks have been proposed for supervised classification and modeling physical systems. In this work, we develop approximately equivariant algorithms in reinforcement learning (RL). We define approximately equivariant MDPs and theoretically characterize the effect of approximate equivariance on the optimal $Q$ function. We propose novel RL architectures using relaxed group convolutions and experiment on several continuous control domains and stock trading with real financial data. Our results demonstrate that approximate equivariance matches prior work when exact symmetries are present, and outperforms them when domains exhibit approximate symmetry. As an added byproduct of these techniques, we observe increased robustness to noise at test time.