Modeling Dynamics over Meshes with Gauge Equivariant Nonlinear Message Passing
Abstract
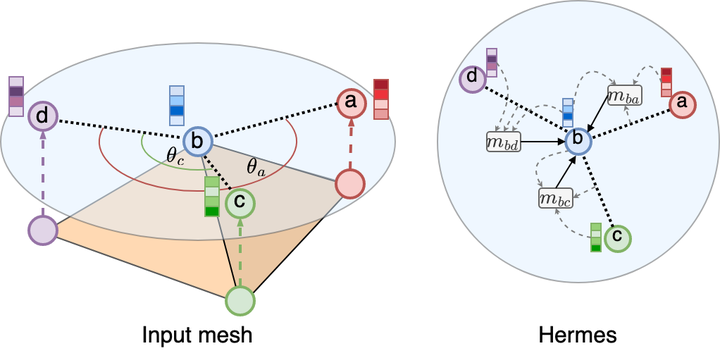
Data over non-Euclidean manifolds, often discretized as surface meshes, naturally arise in computer graphics and biological and physical systems. Of particular interest is solving complex partial differential equations (PDEs) on surfaces. While graph neural networks have been successfully applied to PDEs, they do not incorporate surface geometry and do not consider local gauge symmetries of the manifold. Alternatively, recent work on gauge equivariant convolutional and attentional architectures on meshes leverages the underlying geometry but underperforms in modeling surface PDEs. To address these issues, we introduce a new gauge equivariant architecture using nonlinear message passing over meshes. Our novel architecture achieves higher performance than either convolutional or attentional networks on domains with highly complex and nonlinear dynamics. %Furthermore, we investigate when nonlinear message passing improves over the linear counterparts and offer guidelines on in which situations our method would provide the most benefit. However, similar to the non-mesh case, design trade-offs favor convolutional, attentional, or message passing networks for different tasks; we investigate in which circumstances our message passing method provides the most benefit.